. Introduction
Dating a building or identifying the sequence of its constructive and destructive phases can give thorough information about the development of the building itself, relating it to its historical context. It also allows, in many cases, to deepen our knowledge of the evolution of the construction technologies. The possibility of dating materials whose age is highly correlated to that of the architectural structure itself is therefore desirable. Many dating methods specific for organic and inorganic materials can be applied in the field of construction dating, the main being radiocarbon and luminescence dating, i.e. Thermoluminescence (TL) and Optically Stimulated Luminescence (OSL). TL is a well-established method for absolute dating of brickworks. Nevertheless, sometimes this technique is not able to solve the dating problems of architectural historians because it gives the time elapsed since the firing in kiln (or any comparable later heating). The frequent practice of reuse (Martini and Sibilia, 2006) and the use of unfired natural materials, such as mud bricks or stones, can make TL dating practically useless (Goedicke, 2003). Differently from bricks, mortar is prepared shortly before use and is usually not recycled. For these reasons mortar dating is a promising tool for chronological studies in archaeology and history of architecture. Even radiocarbon could be applied to mortar, dating the carbon dioxide absorbed by the material structure from the atmosphere during the crystallization process (Heinemeier et al., 1997; Konow and Lindroos, 1997; Ringbom, 1997). A number of experiments have been carried out to satisfactorily extract calcite from mortar and date it with AMS (Lubritto et al., 2015; Lindroos et al., 2014; Ringbom et al., 2014; Pesce et al., 2012; Hale et al., 2003) but until now it has not become a routine method, due to the contamination of the anthropogenic calcite with the geogenic one.
Once excluded TL (the TL minerals found in mortars are not subject to any heating), OSL is the best candidate for mortar dating. The basic assumption of this technique is that the quartz used as aggregate is optically zeroed during the process of quarrying and mixing, exposing the grains to sunlight (Zacharias et al., 2002; Goedicke, 2003). The age is obtained through the evaluation of the amount of radiation dose absorbed since the preparation as a consequence of the exposure to the natural radiation field:
While OSL is a well consolidated method for dating sediments (Aitken, 1998) the applications to mortars are still few (Urbanová and Guibert, 2017; Urbanova et al., 2015; Panzeri, 2013; Goedicke, 2011, 2003; Bøtter-Jensen and Murray, 2002; Zacharias et al., 2002). The main problem of this application is the incomplete zeroing of the OSL signal after sunlight exposure. A partial or inhomogeneous bleaching of quartz grains can be due to the presence of quartz of different origin whose bleaching characteristics can highly vary, as well as to the short duration of the exposure to light during the manufacturing process, especially for what concern the mixing and working procedures at the construction site. Further problems arise when dating young buildings, due to an OSL signal close to the threshold of detection (Goedicke, 2011).
For mortar dating the use of the coarse grain fraction was suggested by Goedicke (Goedicke, 2003). In this application to fourteen independently dated mortar samples from Germany he found that the larger the grains, the higher the probability of being well bleached. The multigrain technique, measuring the OSL signal of aliquots consisting in hundreds of quartz grains, gave acceptable values of absorbed dose only with well-bleached samples while it obviously overestimated it in poorly bleached grains. The single-grain procedure (Bøtter-Jensen and Murray, 2002; Murray and Roberts, 1997), based on the OSL signal of each single quartz grain, allows the identification of the best-bleached grains in a heterogeneously and/or incompletely bleached mixture. This technique is highly time-consuming because usually only less than a few percent of the grains give acceptable signals. The analysis of a huge number of grains is therefore required (Goedicke, 2011, 2003; Duller et al., 2000). An appropriate statistic elaboration of the experimental data is then a crucial step and several different approaches have been proposed. They are: 1) the weighted mean, 2) the Central Age Model (CAM, Galbraith et al., 1999), 3) the Minimum Age Model (MAM, Arnold et al., 2009; Galbraith et al., 1999), with slightly modified versions, 4) the Internal-External Consistency Criterion (IEU, Thomsen et al., 2007 and 2003). Their common goal is the identification of the best-bleached fraction in heterogeneously bleached samples, to achieve a reliable evaluation of the true average historical equivalent dose. It seems that the IEU model and the MAM give good results in case of differently bleached samples (Urbanova et al., 2015; Medialdea et al., 2014; Jain et al., 2004).
Aim of this work is to explore the potential of OSL dating of earthen mortars, a particular kind of mortar consisting in quartz-rich aggregate dispersed in silty-clayey matrix, in the light of the results available on lime mortars.
Earthen architecture is widespread mainly in rural areas, with buildings made of rammed earth or mud bricks and mortars (Aubert et al., 2015; Fratini et al., 2011). Sometimes, earthen mortars are also used to bind high quality fired bricks in churches, private buildings and civic architecture. This construction technique is witnessed in Cremona (Northern Italy, Po valley; Cantù et al., 2016; Fieni, 1999; Bonazzi and Fieni, 1995), where the earthen mortars object of this study were sampled from two buildings whose structures were well dated on historical ground. To test the dosimetric properties of the samples we used both the small aliquot multigrain and the single grain OSL protocols (Murray and Roberts, 1997). We also tested and compared the reliability of the main statistical methods used for data elaboration and for final De estimation (Eq. 1.1).
. Materials and methods
Sampling and sample preparation
The earthen mortars analyzed in this study are briefly described in Table 1. They came from two buildings located in Cremona, a small town in the Po valley, Northern Italy: Palazzo Raimondi (PR), built between 1493 AD and 1496 AD and Palazzo Soldi (PS), one of the most important residences of the town until the 15th century. They are similar in size, typology and construction techniques and were chosen for the completeness of the diagnostic investigations, historical surveys and available building stratigraphy. Those aspects allowed identifying mortars belonging to precisely and accurately dated structures: the original construction phase for Palazzo Raimondi (1495 AD) and a late 18th century restoration phase at Palazzo Soldi. The mortar samples were collected without exposing the material to daylight by means of a darkened environment made with a textile and using a red lamp. They were sampled using a chisel and a hammer. First of all the surface layer of the mortar was removed and then the inner part was collected and put into a black plastic bag. The upper and lower bricks in contact with each mortar joint were sampled as well. The mortars were very similar, consisting in an angular to subangular, moderately to poorly sorted, coarse to fine grained quartz-rich aggregate dispersed in a silty-clayey matrix. The matrix (grain size < 63 μm) usually ranged between 5 and 10 wt%, seldom reaching 20 wt%, and was composed of predominant quartz and fresh and/or weathered phyllosilicates. Little amount of carbonates might be present in the fine fraction due to lime addition to the mortars, especially in post-17th century samples. The aggregate (grain size > 63 μm) ranged between 75 and 95 wt%, mainly composed of quartz grains (30–40%), metamorphic rock fragments (mica schist and quartz-rich rocks, 5–30%), feldspars (5–10%), phyllosilicates (5–15%), amphiboles (0–5%), carbonates (0–5%), brick fragments (0–5%) and rare lime lumps (Cantù et al., 2015).
Table 1
List of the analyzed samples with weight and their yield in 150–250 μm quartz.
For OSL measurements, samples were chemically treated, separated and prepared according to the standard procedures (Preusser et al., 2008; Mejdahl, 1985) to obtain the 150–250 μm size quartz fraction. Table 1 also reports the samples weight and their yield in 150–250 μm quartz.
Multi-grain aliquots were prepared by fixing the quartz grains onto 10 mm diameter stainless steel disks with silicon oil (covered area: about 3 mm diameter, corresponding to roughly 300 grains). For the single-grain procedure, the quartz grains were mounted on special 10 mm diameter aluminium disks with a grid of 10×10 holes holding the individual crystals.
OSL measurements and statistic models
OSL measurements were carried out with a Risø TL/OSL DA-20 reader. Photons were detected by a bialkali photomultiplier tube (EMI 9235QB) coupled to a 7.5 mm Hoya U-340 band pass UV filter (280–380 nm). Artificial β irradiations were given using a 90Sr-90Y source delivering 0.13 ± 0.01 Gy/s.
OSL measurements were performed using the single-grain procedure. The small aliquot multi-grain procedure was applied if a minimum of 10 multi-grain aliquots could be prepared.
The multi-grain aliquots were stimulated by an array of blue LEDs (470 ± 30 nm) with a constant stimulation power of 54 mW/cm2 or with IR LEDs (830 ± 10 nm) with a constant stimulation power of 360 mW/cm2. The samples were stimulated at 125°C for 40 s. Single-grain measurements were performed using the single-grain laser attachment of the Risø system. The stimulation source was a 10 mW Nd:YVO4 solid-state diode-pumped laser emitting at 532 nm, which can be focused sequentially on each of the 100 grains mounted on the disk (Bøtter-Jensen et al., 2003). Each grain was stimulated for 1 s at 125°C.
The OSL signal of multi-grain aliquots was obtained integrating the first 0.64 s and subtracting the background signal (mean of the OSL signal of the last 8 s). The OSL signal of single-grains was obtained integrating the first 0.2 s less the background (OSL signal of the 0.7–0.9 s range).
To evaluate the absorbed radiation dose, De (Eq. 1.1), the Single Aliquot Regenerative-dose (SAR) protocol was used (Wintle and Murray, 2006; Murray and Wintle, 2003 and 2000), applying from three to five regeneration doses. A zero dose point was given after the highest regeneration dose measurement cycle to check the recuperation of the signal, followed by the repetition of the first regeneration dose for the recycling test. The purity of quartz samples was tested by OSL post IR measurements (Duller, 2003). The pre-heat temperature was chosen by means of the pre-heat plateau test.
For each sample, many De have to be evaluated, in principle one for each multi-grain aliquot or one for each single-quartz grain. They were estimated using the Risø Analyst 4.31.7 software by interpolating the natural sensitivity-corrected signal onto the dose response curve. The uncertainties associated to such individual De were calculated from counting statistics, curve fitting and assuming an instrumental reproducibility error of 2.5%.
To get the best estimate of the true value of a sample’s De, all the individual values were statistically elaborated using the software R and Luminescence 0.4.4 package (http://CRAN.R-project.org/package=Luminescence), applying the statistics briefly described below:
- Weighted mean, using the individual dose uncertainty as weight (W=1/σ2).
- Central Age Model (CAM, Galbraith et al., 1999). It assumes that the logs of individual De estimates are evaluated from a normal distribution with a standard deviation representing the over-dispersion of the data.
- Minimum Age Model (MAM, Galbraith et al., 1999). It assumes that the sample is composed of two or more populations of grains with different bleaching, leading to a multimodal distribution of De. The De values result from a truncated log-normal distribution, where the lower truncation point corresponds to the average log value of the fully bleached grains (namely the minimum age). The developed versions of MAM (MAM3 and MAM4) differ for the number of parameters used in calculation. In this case MAM3 was used, because the data sets do not always warrant fitting the 4-parameter model. The application of the MAM requires the knowledge of the amount of data dispersion, usually described by the over-dispersion parameter (OD). It corresponds to the σ value of CAM (Galbraith et al., 1999). The over-dispersion is due to both intrinsic and extrinsic factors. Among the first ones are counting statistics, instrument reproducibility, other OSL characteristics of the sample, such as quartz sensitivity, predominance of the fast or slow component, etc., variation in the dose rates at the grain size scale (Urbanova et al., 2015), variation of the dose-rate of the beta source at the level of the 100 holes grid of SG discs (Lapp et al., 2012). The main extrinsic factor is the incomplete bleaching. The intrinsic OD is required as input value to obtain the minimum age.
- un-logged MAM (ul-MAM, Arnold et al., 2009). This model is a modification of MAM, and is based on the assumption that De derives from a normal distribution. It was developed to analyse data sets with zero or negative De values. This situation happens especially in very young samples (< 350 years) and the model is applied to the actual De estimates and their absolute standard error, rather than to their logarithms and their relative errors.
- Internal-External Consistency Criterion (IEU, Thomsen et al., 2007 and 2003). It allows the identification of the proportion of best-bleached grains, assuming that they correspond to the lowest normal-dose population. This model only applies to single-grain results.
. Results and discussion
Annual dose rate measurements and evaluation of the expected De
To obtain the annual dose-rates of Eq. 1.1, the radioactivity of the samples and of the surrounding bricks was measured. These analyses were necessary to evaluate the true value of the De absorbed by the single samples, as described in the following. 238U and 232Th concentrations were derived from alpha counting of the crushed bulk mortars and adjacent bricks using ZnS (Ag) scintillator discs and assuming a Th/U concentration ratio equal to 3.16 (Aitken, 1985). Contribution due to 40K content was obtained from the total concentration of K measured by flame photometry. The saturation water content of both mortars and bricks ranged from 10 to 12%. Taking into account the wet climate of the area and the high humidity conditions at the sampling points, the 75 ± 15% of saturation was assumed for calculations. The attenuation of the beta particles in coarse grain quartz was taken into account (Bell, 1979). The gamma external contribution mainly derives from the radioactivity of a 30 cm diameter sphere centered at the sampling point (Aitken, 1985). Such contribution was evaluated from the radioactivity concentrations of the mortars themselves and of the surrounding bricks (Galli et al., 2014). The contribution of each material to the annual dose-rate was evaluated applying the infinite matrix approximation, with updated conversion factors (Guérin et al., 2011). The radiation-matter interactions are similar in bricks and mortars, since the effective atomic mass Z* is similar in the two materials, and so do the mass attenuation coefficients (evaluated to approximately 3·10–2cm2/g at 2.5 MeV). To model our system we considered a sequence of homogenous 50 mm thick bricks assembled with 10 mm-thick mortar layers, as obtained after in situ measurements. In these conditions the brick contribution to the external dose rate within the interaction sphere does not exceed 40%.
The main results of radioactivity measurements are reported in Table 2, together with the resulting dose-rates, including a 0.15 mGy/a cosmic ray contribution (Prescott and Hutton, 1994).
Table 2
Radioactivity concentration in mortars (column 2–4) and bricks (column 5–7), derived annual total dose rates and calculated expected De.
Because both the annual dose-rate and the age of the samples are known, their true De can be derived by the inverse formula of Eq. 1.1:
Such De are obtained by multiplying the data of column 4 of Table 1 by those of column 8 of Table 2. They are listed in Table 2, column 9. They have been taken as reference values to which compare the experimental results given by the different experimental protocols and/or statistic elaborations, and referred to, in the following, as expected De.
Multi grain technique De
The multi-grain protocol was used for the six mortars listed in Table 3, those for which more than ten quartz aliquots could be prepared. Individual De values were rejected if one of the following criteria was not satisfied: recycling ratio between 0.9 and 1.1, recuperation < 5%, IR test < 10%.
Table 3
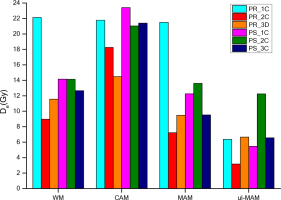
Multi-grain technique: Expected De and De evaluations with different statistical models.
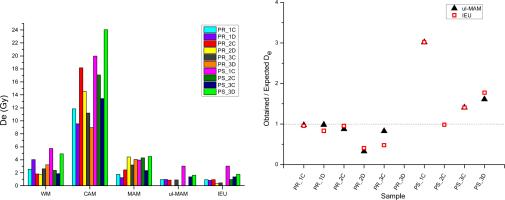
Eventually, the percentage of acceptable aliquots ranged from 40 to 70%, as shown in Table 3, also reporting the De results given by weighted mean, CAM, MAM and ul-MAM models. The same results are visualized in Fig. 1, grouped by model and normalized to the expected De.
Fig. 1
De obtained with multi-grain technique calculated with different statistical model and normalized to expected De.
All the models overestimate the De, CAM giving the worse results. Regardless the statistic model used for data elaboration, the multi-grain protocol gives De values higher than expected, which will lead to a significant and systematic age overestimation. This is reasonably caused by an ineffective or inhomogeneous bleaching of the quartz grain. This can be due to the presence of hard to bleach grains and/or insufficient exposure to sunlight during the preparation of the mortar. Whatever the reason, the quartz grains did not receive enough sunlight to fully erase the luminescence signal acquired over geological time and the bleaching process results in an incompletely and heterogeneously reset grain mixture. The multi grain technique is therefore unsuitable for this typology of samples.
Single-grain technique De
For the single-grain analysis, between 3200 and 4800 grains for each sample were measured. The percentage of grains giving a detectable OSL signal ranged between 15 and 25% (Table 4, 4th column). Even if relatively bright, the grains were rejected if one of the following conditions occurred: the signal was less than 3 standard deviations above the background, the recycling ratio was out of 0.75–1.25 range, the error associated to the test dose was >25%, the dose response curve determined from laboratory regeneration doses did not intersect with the natural signal. In such a way, less than 4% of the grains could be used for De evaluation (Table 4, 5th column).
Table 4
Single-grain technique: expected De and De evaluations with different statistical models.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample | Expected De (Gy) | # Measured grains | # Bright grains (%) | # Accepted grains (%) | OD De (a) (%) | OD Drt b (%) | De Weighted mean (Gy) | De CAM (Gy) | De MAM (Gy) | De ul-MAM (Gy) | De IEU (Gy) |
| PR_1C | 1.13 | 4800 | 18 | 1.8 | 128 | 19 | 2.9±0.12 | 13.4±2.0 | 2.0±0.4 | 1.1±0.2 | 1.08 0.16 |
| PR_1D | 1.12 | 3800 | 24 | 1.3 | 150 | 20 | 4.52±0.05 | 10.7±2.5 | 1.4±0.4 | 1.1±0.2 | 0.93±0.16 |
| PR_2C | 1.26 | 3800 | 20 | 1.2 | 106 | 29 | 2.3±0.2 | 22.9±3.2 | 3.1±0.8 | 1.1±0.3 | 1.2±0.2 |
| PR_2D | 1.23 | 4100 | 22 | 2.0 | 81 | 20 | 2.6±0.2 | 22.0±2.3 | 6.7±1.2 | ND | 0.5±0.2 |
| PR_3C | 1.09 | 4200 | 23 | 2.6 | 99 | 30 | 2.85±0.12 | 12.2±1.3 | 3.5±0.7 | 1.0±0.3 | 0.52±0.15 |
| PR_3D | 0.96 | 4000 | 19 | 2.2 | 91 | 24 | 3.12±0.09 | 8.6±0.9 | 3.9±0.5 | ND | ND |
| PS_1C | 0.53 | 3200 | 21 | 3.6 | 109 | 20 | 3.05±0.07 | 10.6±1.2 | 2.1±0.3 | 1.6±0.2 | 1.6±0.14 |
| PS_2C | 0.58 | 4700 | 14 | 0.9 | 91 | 30 | 1.39±0.13 | 9.9±1.7 | 2.5±0.7 | ND | 0.57±0.18 |
| PS_3C | 0.64 | 4200 | 15 | 0.7 | 137 | 20 | 1.2±0.2 | 8.6±2.5 | 1.5±0.6 | 0.9±0.2 | 0.9±0.2 |
| PS_3D | 0.62 | 3900 | 21 | 1.7 | 109 | 20 | 3.06±0.17 | 14.9±2.2 | 2.8±0.6 | 1.0±0.2 | 1.1±0.2 |
The radial plots and the distributions of the individual De obtained for the 10 mortar samples are visualized in Fig. 2 (Palazzo Raimondi) and Fig. 3 (Palazzo Soldi), showing a high dispersion with De values up to hundreds of Gy. These data were elaborated to get the best estimate of the the sample’s De according to the various statistical models. The De results obtained with the weighted mean are from to 2 to 5 times higher than expected, the mean error being about 6%. The CAM (Table 4, column 9th) gives results approximately 10 to 20 times higher than expected, with higher errors (10–30%). The over-dispersion parameter (OD) is also reported in Table 4, column 6th. It corresponds to the standard deviation value of the CAM De (Galbraith et al., 1999). The intrinsic De over-dispersion, required for the application of both the Minimum Age Model and the Internal-External Consistency, is also shown in Table 4, column 7th. It was measured with the dose recovery test (Urbanova et al., 2015). The grains were individually bleached by double green light illumination intercalated to a 10000 s pause. A known beta dose (2.58 ± 0.05 Gy) was given to the sample and subsequently measured. The OD values so obtained varied between 20 and 30%, being considerably lower than the over-dispersion of the archaeological De (see Table 4, 6th column). The contribution of the extrinsic factors to the OD is therefore consistent, indicating the incomplete bleaching as the responsible of the observed huge spread of De.
Fig. 2
a–f. Radial plots and histograms of De distribution for the mortar samples of Palazzo Raimondi (a and b: PR_1C; c and d: PR_1D; e and f: PR_2C).
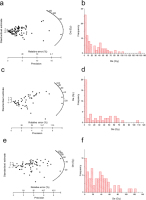
Fig. 2
g–l. Radial plots and histograms of De distribution for the mortar samples of Palazzo Raimondi (g and h: PR_2D; I and j: PR_3C; k and l: PR_3D).
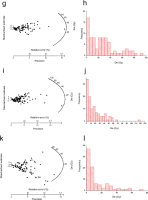
Fig. 3
a-f.Radial plots and histograms of De distribution for the mortar samples of Palazzo Soldi (a and b: PS_1C; c and d: PS_2C; e and f: PS_3C).
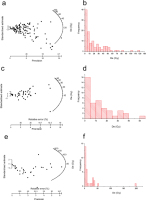
Fig. 3
g-h. Radial plots and histograms of De distribution for the mortar samples of Palazzo Soldi (g and h: PS_3D).
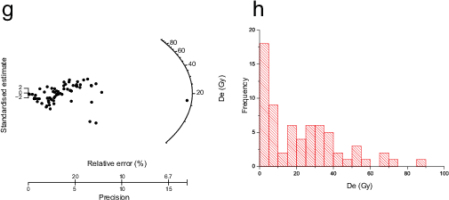
The results of the MAM (column 10th Table 4) were always higher than expected while those of un-logged MAM (column 11th Table 4) were consistent (±1σ) with the expected ones for five samples out of ten. The same was found with the IEU model (column 12th Table 4), for which the OD calculated with the dose recovery test was added in quadrature to the uncertainties of each individual De (Thomsen et al., 2012, 2007 and 2003). All the De results of Table 4, normalized to the expected De, are visualized in Fig. 4a, grouped by method. Fig. 4b shows only the results of ul-MAM and IEU.
. Conclusions
OSL dating was applied to earthen mortars from Cremona, consisting in a quartz-rich aggregate dispersed in silty-clayey matrix. The aim of this study was to explore the most suitable methods for equivalent dose evaluation for mortars and such an investigation required a set of known age samples. They were taken from two well independently dated structures (Palazzo Raimondi: 1495–1499 AD and Palazzo Soldi: 1770–1790 AD). In this study we applied the multigrain and the single grain protocols for dose evaluation to quartz samples separated from ten well-dated earthen mortars, six from Palazzo Raimondi and four from Palazzo Soldi; the reliability and effectiveness of the various statistical methods in identifying the best-bleached samples were tested. The comparison of the results allows making the following considerations.
The multi-grain protocol gives De values higher than expected, leading to a significant and systematic age overestimation. This means that the quartz grains did not receive enough sunlight to fully erase the luminescence signal acquired over geological time. Hence, the resetting process results in an incompletely and heterogeneously reset grain mixture. In order to circumvent this problem, the single-grain protocol was applied. The majority of grains (about 80%) was rejected due to the very low signal-to-noise ratio. Within the analysed grains, after applying the rejection criteria previously described, less than 3.5% were accepted for dose evaluation. The De obtained with single-grain procedures showed a large De distribution confirming that samples are likely still retaining part of their geological signal. Since De are highly dispersed and the samples are very likely affected by heterogeneous bleaching, it is not surprising that De were overestimated by the methods including all the dose points (weighted mean and CAM). The MAM and IEU are therefore expected to better evaluate the true equivalent dose. In many cases the log-MAM3 overestimates the De and only for one sample (PR1D) the De obtained is in agreement with the expected one. It was found that, in all cases, the un-log MAM3 and IEU model give the better estimation of the mortar expected age, even if the precision of the method is still relatively low.
In conclusion, this study highlighted the potentiality of the OSL single grain technique for mortar dating. At the same time, it revealed the limit of this method to achieve accurate and precise results.