. INTRODUCTION
Luminescence in all forms, namely thermoluminescence (TL), infrared stimulated luminescence (IRSL) and optically stimulated luminescence (OSL), arises from band to band transitions and impurity ions or intrinsic defects. These impurities inside the matrix of the luminescence materials give rise to localised energy levels within the forbidden energy band gap. Luminescence dosimetry nowadays represents a key technique in absorbed dose measurements (Furetta, 2003). While IRSL and OSL are mostly used for dosimetry/dating purposes, TL is an experimental technique used in diverse scientific disciplines, which, besides dosimetry, include archaeology, geology, medical and solid state physics. It is well known that every geological inorganic material, insulator or semiconductor, which has been previously exposed to ionising radiation, could be a potential luminescent dosimeter in action; in other words, it could yield luminescence signal. The process in which absorbed energy is converted into luminescence light can be distinguished in different steps, each one characterised by certain efficiency. Materials with high total efficiency are characterised as sensitive TL dosimeters (TLDs) (Bos, 2001).
Nowadays, the term oxidation refers to all processes involving the loss of electrons. Nevertheless, originally the word oxidation implied a chemical reaction with oxygen to form an oxide since the gas O2 was historically the first recognised oxidising agent. For many areas of materials science, a reaction in the presence of O2, and thus subsequent degradation, stands as one of the primary instability mechanisms. For instance, in practical thermoelectric applications, apart from high efficiency, excellent thermal stability at the intended operating temperature range is of vital importance (Yin et al., 2015). Thus, degradation of high-temperature Mg2Si thermoelectric devices through oxidation is one of the primary examples in the field of thermoelectrics, as in the presence of O2, Mg2Si decomposes to form MgO and Si (Tani et al., 2009). Nevertheless, while for the field of thermoelectrics, the presence of oxides is not welcome for the operational stability, in the field of TL dosimetry, a variety of oxides have been effectively applied as sensitive TLDs. Aluminium oxide (Al2O3:C) (Akselrod and Kortov, 1990; Markey et al., 1995) and beryllium oxide (BeO) (Sommer and Henniger, 2006; Sommer et al., 2007, 2008; Yukihara, 2019a, 2019b; Aşlar et al., 2019) stand among the most distinguished members of this list; for an extended review on the oxides used as TLDs, the readers could refer to McKeever et al. (1995).
Magnesium oxide (MgO), in its un-doped form, also yields sufficient TL sensitivity. Its potential applicability in TL dosimetry was exploited many decades ago (Roessler and Walker, 1967; Ziniker et al., 1973; Takeuchi et al., 1976; Carter, 1976). Nevertheless, due to a number of reasons, which include (a) composite glow curve structure, (b) relatively low sensitivity and (c) high variability of its TL properties depending on the synthesis technique, magnesium oxide has not found wide acceptance as a practical TL detector. Some of the earlier results have been reviewed by McKeever et al. (1995). Many researchers aimed towards optimisation of its luminescence properties, by adopting different synthesis methodologies as well as doping (Bapat and Sivaraman, 1985; Bapat et al., 1985; Dolgov et al., 2002; Bos et al., 2006; Oliveira et al., 2013). According to a recent report, using a combination of the Solution Combustion Synthesis (SCS) method, doping with different lanthanides (Ln) and co-doping with lithium (Li) can considerably increase the sensitivity of MgO (Orante-Barron et al., 2011). Nevertheless, according to this latter citation, the lanthanide doping was reported to affect not only the luminescence centres but also the shape of the TL curve. An extensive review of the defects in MgO and their relationship with its TL properties can be found in Las and Stoebe (1984).
The present work attempts a correlation between TL and OSL signals observed in MgO phosphor via a bleaching study. By the term bleaching, we refer to the effect of the eviction of a significant proportion of the trapped electrons abandoning thus the traps when the dosimeter is exposed to artificial or natural light. The physical mechanisms that govern the effect of bleaching are yet to be thoroughly understood. Moreover, even though the bleaching properties of TL traps in various materials seem to be a both unmapped as well as very important topic of research from a physical point of view, very few related works have been reported so far in the literature. Among these, special emphasis should be addressed to those reported by Spooner (1994) and Kitis et al. (2010) for the case of quartz and Dallas et al. (2010) for the case of KMgF3:Ce3+. Very recently, Sfampa et al. (2015), Kitis et al. (2016) as well as Angeli et al. (2019) have individually attempted correlation of basic TL, OSL and IRSL properties of various K-feldspar samples and other geological samples. According to those mentioned above, scanty reports of related literature, all luminescence forms make use of the same traps, namely TL traps. Further establishing this latter experimental statement/feature becomes the primary aim of the present study.
. EXPERIMENTAL PROCEDURE
Sample, apparatus and measurement conditions
The study was performed on natural magnesium oxide sample, MgO. This specific sample was selected mainly for two reasons: (a) the convenient shape of its glow curve, consisting of two, prominent and independent groups of overlapping peaks and (b) the lack of any previous related studies on this specific material. The commercial MgO sample was purchased from Sigma Aldrich. Grains of dimensions between 80 μm and 140 μm were obtained after dry sieving. Aliquots with the mass of 5 mg each were prepared by mounting the material on stainless-steel disks of 1 cm2 area. Mass reproducibility was kept within ±5%.
All luminescence measurements were carried out using a Risø TL/OSL Reader (model TL/OSL–DA–20), equipped with a high power blue LED light source (470 nm, FWHM 20 nm delivering at the sample position a maximum power of 40 mW/cm2) and a 90Sr/90Y beta particle source, delivering a nominal dose rate of 0.1083 Gy/s (Bøtter-Jensen et al., 2000). A 9635QB photomultiplier tube with a Hoya (U-340) blue filter was used for light detection (340 nm, FWHM 80nm). All TL measurements and heatings were performed in a nitrogen atmosphere with a low constant heating rate of 1°C/s, in order to avoid significant temperature lag (Kitis et al., 2015); TL measurements were performed up to the maximum temperature of 500°C. OSL measurements were performed in both continuous wave as well as linearly modulated configurations (CW-OSL and LM-OSL, respectively). In the former case, the power level was software controlled and set at 90% of the maximum stimulation intensity for blue LEDs. For LM-OSL curves (Bulur, 1996), the ramping rate was 0.04 mW/cm2/s, increasing the stimulation light power from zero up to the maximum power (40 mW/cm2) for 1000 s.
Experimental Protocols
Bleaching can take place in nature either spontaneously or under strict experimental conditions. In the latter case, measuring the number of optically de-trapped electrons that are emitted following stimulation, results in optically stimulated luminescence (OSL) curves. In the framework of the present study, bleaching was performed by exposing the samples to the blue LEDs housed inside the Risø commercial TL/OSL Reader, stimulating at 90% of their maximum stimulation intensity (40 mW/cm2, Bøtter-Jensen et al., 2000). Similar bleaching studies were also performed in the past for the case of quartz (Polymeris et al., 2012). The experimental procedure involved two basic protocols. The first one (protocol A) was applied in order to investigate the bleaching of the entire glow curve; therefore the OSL measurements were performed at room temperature (RT hereafter), according to the following protocol that consists of the following steps:
Step 0: Test Dose and TL measurement for the un-bleached signal in order to monitor the un-bleached signal.
Step 1: Test Dose and CW-OSL measurement for stimulation time ti=1 s.
Step 2: TL measurement in order to obtain the residual TL.
Step 3: Steps 1&2 were repeated using different stimulation times ti= 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 and 2048 s.
The second protocol (protocol B) was applied in order to investigate the bleaching of the high temperature part of the glow curve. In this case, the protocol mentioned above was applied, after incorporating the following two modifications; (a) before each OSL measurement, a TL up to 180°C was performed, in order to empty all shallow traps and (b) the OSL measurements were performed at 170°C in order to prevent re-trapping of charge evicted from the deeper traps into shallow peaks.
The test dose applied was 20 Gy. According to the related literature, MgO does not yield sensitivity changes following successive cycles of irradiation and TL measurements. Therefore, each one of the protocols described above was applied to two independent aliquots, implying thus a single aliquot procedure. Nevertheless, performing sensitivity variation tests was inevitable. Three sensitivity tests were performed by recording a TL glow-curve for a test dose of 20 Gy, one after the RTL corresponding to 8 s bleaching, one after the RTL corresponding to 128 s bleaching and one, final, after the final step of 2048 s bleaching. The resulted TL glow-curves showed a reproducibility within 2%, which means that there is no need for sensitivity corrections. Finally, after the application of each protocol characteristic LM-OSL curves were obtained for a stimulation time of 1000 s.
. METHOD OF ANALYSIS
The entirely empirical general order kinetics can be considered as an approach to the elementary OTOR model (Sadek et al., 2014a, 2014b). Recently, Kitis and Vlachos (2012) showed that the OTOR system of differential equations can be solved analytically using the Lambert W(z) function. The analytical expression derived by them is advantageous, because it is a general equation describing all commonly used luminescence stimulation modes. In other words, the same equations can describe TL, linearly modulated OSL (LM-OSL), continuous wave optically stimulated luminescence (CW-OSL), Isothermal TL (ITL) and others, by just setting the corresponding stimulation mode.
The original equation derived by Kitis and Vlachos (2012) as a solution of the OTOR model is the following:
where N is the total concentration of trapping states and W(z) is the Lambert W function (Corless et al., 1996), and R=An/Am with An, Am being the re-trapping and recombination coefficients correspondingly. In the present work Eq. 3.1 will be used considering only the case R < 1 (Corless et al., 1996; Kitis and Vlachos, 2012, Sadek et al., 2014a). The function p(t, T) in Eq. 3.1 deals with the stimulation mode used during the experiments. For the case of TL is p(T) = s·exp(−E/kT) so, the argument z of the Lambert function W(z) becomes:For the case of LM-OSL, p(T) = λt so, the argument z of the Lambert function W(z) becomes:
For the case of exponential decay, p(T) = λ so, the argument z of the Lambert function W(z) becomes:
In the case of TL the original Eq. 3.1 was transformed by Sadek et al., (2014b), so that the parameters N and s were replaced by the maximum TL intensity of the peak Im and by the temperature of the peak maximum Tm. This is a very useful substitution, since these two quantities Im and Tm can be obtained directly and accurately from the experimental TL glow curves.
The final equation (given by Sadek et al., 2014b) is the following:
where z is now approximated by the expression: and zm is the value of z for T = Tm according to Eq. 3.6.Eqs. 3.5 and 3.6 are the analytical equations used to fit the experimental TL glow curves, with the two adjustable fitting parameters being the activation energy E and the ratio R (with R < 1).
The function F(T,E) in this expression is the exponential integral appearing in TL models and is expressed in terms of the exponential integral function Ei[− E/kT] as (Chen and McKeever, 1997; Kitis et al., 2006):
For the LM-OSL we have:
where z is now approximated by the expression: and zm is the value of z for t = tm according to Eq. 3.9.The application of the Lambert function W(z) is quite complicated when one has to use analytical approximations for it (Kitis and Vlachos, 2012). On the other hand, its application is very simple in commercial software packages (for example MATHEMATICA, MATLAB) which include it as a built-in function, similar to any other transcendental function. In the present work, the ROOT data Analysis Framework was used (ROOT, 2015). All fittings were performed using the MINUIT program (MINUIT, 2015) released in ROOT, which is a physics-analysis tool for function minimisation. The Lambert function W(z) and the exponential integral function Ei[−E/kT] are implemented in ROOT through the GNU scientific library (GNU GSL) (GNU, 2015). The goodness of fit was tested using the Figure Of Merit (FOM) of Balian and Eddy (1977) given by:
The FOM index value provides a measure for the goodness of fit; the lowest its value, the best fit we get. Therefore, every fitting attempt should result in minimising the FOM index value, which was achieved by changing the set of parameter values of each glow peak.
. RESULTS AND DISCUSSION
Experimental luminescence curve shapes
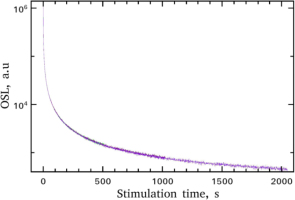
As it is seen from the experimental protocol, the bleaching of the TL glow-curve of MgO is achieved through CW-OSL stimulation. All these CW-OSL curves were recorded; typical shapes of these are shown in Fig. 1. The latter figure contains the normalised CW-OSL curves corresponding to stimulation times of 128, 256, 512, 1024 and 2048 s, which coincide. This experimental fact is a direct evidence of the excellent reproducibility of the measuring sequence. The most interesting detail of these curves is the very fast decay in short stimulation times. The same results are also observed for the rest of the CW-OSL curves obtained.
Fig. 1
CW-OSL decay curves received at room temperature, using blue light for stimulation times 128, 256, 512, 1024 and 2048 s, which coincide. This experimental feature yields the excellent reproducibility the measuring sequence.
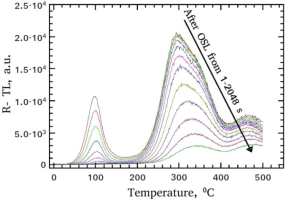
The shapes of residual TL (R-TL) glow-curves as a function of the bleaching time from 1 to 2048 s are shown in Fig. 2. The TL glow-curve has a characteristic low temperature glow-peak and a number of overlapped high temperature glow-peaks. Similar are the shapes for the case of the OSL curves after preheat at 170°C, without yielding the shallow peak at around 100°C. According to the data of this latter plot, it is possible to conclude that the shallow trap responsible for the low temperature TL peak is easily and fast bleached within stimulation time intervals between 2 s and 20 s. On the contrary, the overlapping peaks located at higher temperatures survive for small stimulation times. Nevertheless, for stimulation durations longer than 100 s, this complex TL peak is also substantially bleached.
Fig. 2
Shapes of the R-TL glow-curves received after bleaching with blue light for all stimulation times, ranging between 1 and 2048 s.
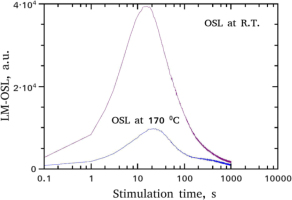
Studying a tentative correlation between the individual TL peaks and OSL components requires the complete analysis of the complex TL glow-curves, which will be presented in detail in section 4 – Analysis of TL glow-curves. Fig. 3 shows the shape of the LM-OSL curves corresponding to each one of the two protocols. The basic characteristic is the very intense fast component obtained in very short stimulation times, exactly as in the case of CW-OSL shown in Fig. 1.
A very interesting result is the quantitative relationship between the integrated signals of the TL-glow-curves and the CW-OSL curves depicted in Fig. 4. The relationship is expressed in terms of the ratio between the integrated OSL signal over the integrated TL-lost signal, where TL-lost is the difference between the un-bleached glow-curve minus the bleached glow-curve at each bleaching (OSL stimulation) time. This difference corresponds to the number of electrons which are getting free due to optical bleaching, which recombining gives the CW-OSL intensity. Therefore, from a phenomenological point of view, it is expected that the ratio will always take values around unity. This theoretical expectation is not verified by the experiment mainly at very short OSL stimulation durations.
Fig. 4
The ratio of integrated CW-OSL over the TL-lost during the various stimulation times. The TL-lost is defined as the difference between the total integrals of the un-bleached glow-curve minus the bleached TL glow-curves (a) For OSL measured at RT and (b) for OSL measured at 170°C.
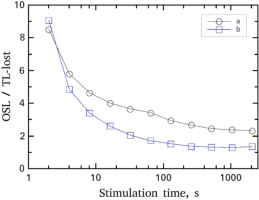
As it is seen in Fig. 4, the integrated CW-OSL signal is much higher than the corresponding TL-lost in both stimulation temperatures for stimulation times less than 20 s. As the stimulation time increases, the ratio tends to unity, in agreement with the theoretical predictions. The direct conclusion concerning the first 20 s of stimulation is that the very high intensity CW-OSL signal corresponds to negligible variation of R-TL curves in the region of the high temperature glow-curve (200–500°C). This observation is crucial for the subsequent analysis of the data and for the final conclusions on the TL and OSL correlation in next sections.
Analysis of TL glow-curves
Twelve (12) R-TL glow-curves were obtained in the framework of protocol 1; these are presented in Fig. 2 along with the corresponding twelve (12) glow-curves obtained in the framework of the protocol 2. Both sets of R-TL curves were analysed using a computerised glow-curve de-convolution (CGCD) using Eq. 3.5 with z according to Eq. 3.6. Furthermore, the CGCD analysis was also performed using the equations for conventional general order kinetics by Kitis et al. (1998). The FOM values obtained were below 1% up to bleaching (stimulation) time of 256 s and between 1 and 2% for bleaching times 512, 1024 and 2048 s. The higher FOM values for the latter cases could be explained by the fact that, due to prolonged bleaching, the intensity of the TL glow curve becomes of poorer statistics. The values of the trapping parameters obtained throughout the fitting analysis are shown in Table 1. The fit of the glow-curves of both protocols was performed with a remarkable stability of the free parameters E and Tm. Furthermore, an excellent agreement between the results of OTOR analytical TL equation and general order kinetics equation was achieved. The errors of E and Tm represent errors of the mean value between the results of the two equations used. Their meaning is twofold, providing besides the error values also the degree of agreement between OTOR analytical equation and general order equation. The agreement achieved was necessary because the general order is an empirical approach of the OTOR analytical equation; as it was shown in detail by Sadek et al. (2014a, 2014b) for R < 1 their differences are negligible. Furthermore, Table 1 shows the values of re-trapping to recombination probability ratio, R, the kinetic order b and finally the percentages of the individual TL peaks for un-bleached glow-curves without and with pre-heat at 180°C.
Table 1
The values of the trapping parameters of MgO resulting from the CGCD analysis using both general order kinetics and OTOR analytical equation.
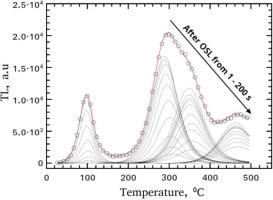
Fig. 5 presents the results of CGCD analysis of the glow-curves from protocol 1. The experimental points (presented as open circles) and the fitted line are given only for the R-TL after 1 s OSL bleaching. The glow-peaks with continuous lines correspond to the CGCD results of all other R-TL glow-curves shown in Fig. 2. The two very low intensity glow-peaks 2 and 3 at 134 and 194°C respectively, are not included in the figure. The integrated signal of each of the peaks in Fig. 5, as well as the sum of the peaks 2 and 3, will be used for the forthcoming analysis in next section.
Fig. 5
Results of the CGCD analysis of RTL glow-curves after CWOSL at RT using Eqs. 3.5 and 3.6. The open circles represent the experimental glow-curve after CW-OSL for 1 s. The line through the experimental points is the fitting line. The continuous lines present the results of the CGCD of all R-TL glow-curves of Fig. 2 without the repeating of the experimental curves. The results for fitting parameters are listed in Table 1.
Analysis of R-TL decay curves
The plot of R-TL signal versus bleaching time has the form of decay curve. Since the decay of R-TL is caused by the optical bleaching, despite its thermal stimulation origin, it reflects the optical bleaching dynamics. For this reason, the analysis of R-TL versus bleaching time will be performed with analytical expressions describing OSL decay curves such as Eq. 3.1 with z from Eq. 3.4. Furthermore, the RTL decay analysis was also performed using the conventional general order kinetics equation (Bulur, 1996). Since, as it was stated above, the R-TL decay behaviour reflects the bleaching dynamics, it is expected that the lifetimes of Table 2 should be related to the lifetimes yielded using the general order kinetics equation by Bulur (1996). It must be noticed, however, that Bulur's equation for CW-OSL is, typologically, identical with the general order kinetics equation describing the decay of TL at a constant temperature. Similarly, Eq. 3.1 with z from Eq. 3.4 also describes the TL decay at a constant temperature. The difference is that in OSL the decay constant represents the optical photoionisation cross-section and in TL decay thermal escape probability.
Table 2
The fitting parameters of the RTL integrated signals as a function of the bleaching time using both general order and OTOR analytical equations. The values are the mean between of the values obtained by the two different equations. The error values provide a strong indication towards the agreement of the two different Equations used.
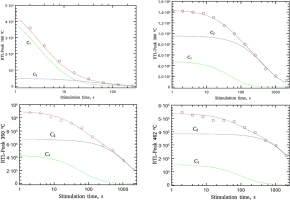
As it is shown in Fig. 5, the CGCD analysis gives the individual TL peaks of the glow-curve. The integrated signal of each peak is plotted as a function of the bleaching time and then fitted using Eq. 3.1 with z from Eq. 3.4 and equation from Bulur (1996). It was not possible to fit the R-TL versus bleaching time using one component, so two components C1 and C2 were used, making thus the analysis very sensitive. Fitting examples are given in Fig. 6. The fitting parameters are listed in Table 2. As is the case of TL CGCD results listed in Table 1 (section 4 – Analysis of TL glow-curves) the values of the lifetime correspond to the mean between the results of OTOR analytical expression and general order kinetics. The error value is again a measure of the agreement between the OTOR decay equation and general order kinetics decay equation.
Fig. 6
Analysis examples of R-TL decay curves based on the integrated signal of the main R-TL glow-peaks resulted from CGCD analysis shown individually in Fig.5. The fit was performed using Eqs. 3.1 and 3.4. The results of the fitting parameters are listed in Table 2.
Since the R-TL decay behaviour reflects the bleaching dynamics, it is expected that the lifetimes of Table 2 should be related to the lifetimes from an analysis of an LM-OSL curve. In the present work, LM-OSL curves were obtained for a simulation time of 1000 s. Their analysis is presented in the next section.
Analysis of the LM-OSL curves
Both LM-OSL curves received at RT and at 170°C, were analysed through a CGCD procedure using Eq. 3.8 and z according to Eq. 3.9. Alternatively, as in the CGCD of TL, the general order kinetics equation of Bulur (1996) as it was modified by Kitis and Pagonis (2008), was used. The analysed LM-OSL curves are shown in Fig. 7, whereas the fitting parameter values are listed in Table 3. Additionally, the percentage of each component for the two LM-OSL curves are presented below. The free parameter tm in column 2 was transformed into a lifetime in column 3 using the conditions for the maximum which as it was shown by Kitis and Vlachos (2012), providing thus identical results for both OTOR analytical equation and Bulur's (1996) general order kinetics equation. The values of the parameter tm and of the per component percentage, as in the previous cases, is the mean between OTOR and general order kinetics equations, whereas its error is a measure of their agreement.
Fig. 7
Component resolved of LM-OSL curves received at RT and at 170°C after a pre-heat at 180°C, using Eqs. 3.8 and 3.9. The results of the fitting parameters are listed in Table 3.
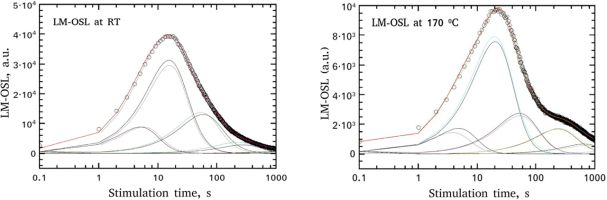
Table 3
The fitting parameters from the analysis of the LM-OSL curve using both general order and OTOR analytical equations. The values are the mean between of the values obtained by the two different equations. Error values provide a strong indication towards the agreement of the two different Equations used.
TL and OSL correlation
A tentative correlation will be based on the comparison of the results of Tables 2 and 3. Obviously, a correlation cannot be achieved just by setting the requirement of exactly equal lifetimes (τ values), because (a) the physical meaning of the lifetime τ is not exactly similar in R-TL and LM-OSL and (b) the values of LM-OSL strongly depend on the total LM-OSL stimulation time. On the other hand, the values must not differ appreciably because both R-TL and LM-OSL take place in the same time interval. A correlation will be attempted by trying to detect the values of LM-OSL curves (Table 3) in the values of R-TL decay curves (Table 2).
Components C1 and C2
The origin of the very fast components C1 and C2 of the LM-OSL curves shown in Fig. 7 become of great interest; the corresponding fitting parameters are listed in Table 3. In the case of LM-OSL measured at RT, these components appear in the LM-OSL curves, because the stimulation power starts from very low value. On the contrary, in the case of CW-OSL the stimulation power takes its highest value immediately. The result is that in CW-OSL curves, these components contribute only to the first second of stimulation, so they cannot be resolved. On the other hand during the two seconds of CW-OSL stimulation when these components have been exhausted due their short lifetime, only the TL intensity of the R-TL for the TL peak at 102°C is reduced, whereas the higher temperature TL peaks have been not influenced at all.
A correlation of these components with the 102°C TL peak is not possible, because these components also appear in LM-OSL curves received at 170°C after a pre-heat up to 180°C, which erases this latter TL peak completely. Finally, as it can be easily seen in Table 3, these components with the percentage of 25% of the total LMOSL signal are related to a negligible TL-lost. So, the net conclusion is that resolution of the correlation method used in the present work is not capable of detecting any relation between the energy levels responsible for the TL peaks and the energy levels responsible for the components C1 and C2 of the LM-OSL signal.
Component C3
Component C3 is very well correlated with the TL peaks at 102, 135 and 194°C. These peaks contribute almost 16% of the TL signal and 25.2% of the LM-OSL signal received at RT. However, although these peaks are erased by the pre-heat at 180°C, component C3 appears also at LM-OSL received at 170°C, representing the 18% of the corresponding signal. Therefore, component C3 originates not only from the peaks with delocalisation temperatures of 102°C, 135°C and 194°C. On the other hand the analysis of R-TL from high temperature peaks does not yield its presence in the region of the high temperature TL glow-peaks. The reason lies behind the resolution of the method. Indeed, component C3 having a lifetime of 4 s is decayed up to OSL stimulation time of less than 20 s. However, as it is seen in Fig. 2, the decreases of the R-TL signal from 1 to 16 s is very weak, so this component cannot be resolved accurately by the method used.
In the case of LM-OSL curve obtained at RT, the components C1, C2 and C3 correspond to the 60% of the total LM-OSL signal. Subtracting the 15% which corresponds to the TL peaks of 102°C, 135°C and 194°C, then a percentage of 45% of the LM-OSL signal cannot be directly correlated, by the method used, with any other TL peak. In the case of LM-OSL recorded at 170°C, components C1, C2 and C3 correspond approximately the 35% of the total LM-OSL signal. Taking into account that the peaks 102°C, 135°C and 194°C are erased by the pre-heat at 170°C then the entire percentage of 35% of these components cannot be related, by the method used, to any of the TL peaks.
Component C4
Another question deals with whether the values of lifetimes τ1 of the peaks at 292°C, 353°C and 464°C could be reflected to the component C4. In order to answer to this question, a discussion about the resolution of the LM-OSL curves is necessary. In a detailed resolution study, Kitis and Pagonis (2008) showed that two overlapping LM-OSL peaks can be resolved if their time at peak maximum intensity, tm, differs by more than 15%. Based on this resolution value and as it is seen in Table 2, the lifetimes of the corresponding to the R-TL decay of peaks at 292 and 464°C are quite close to each other. Taking also into account that the contribution of the TL peak at 292°C is much higher, then it can be easily concluded that their discrimination in LM-OSL curve is very difficult. On the other hand, corresponding to the TL peak at 353°C is quite different but with relatively low contributions. So, the conclusion concerning the LM-OSL curve received at RT cannot be more than a quantitative relationship of LM-OSL component C4 with the first component of the R-TL decay curves.
Concerning the LM-OSL curves received at 170°C after a pre-heat to 180°C, the lifetime values τ1 are very close to the lifetime value of LM-OSL component C4. So, in this case it is quite safe to correlate the first component of the R-TL decay curves of TL peaks at 292°C, 353°C and 464°C, with the component C4 of the LM-OSL curve.
Component C5
In the previous sections, a correlation based only on the first component of the R-TL decay curves was discussed. The reason is that the lifetime of the second R-TL component is equal and mainly greater than the LM-OSL stimulation time. This means that these components should correspond to LM-OSL peaks having peak maximum (tm) at times beyond the 1000 s. The consequence is that in LM-OSL only the rise part of such high tm LM-OSL peaks is recorded without any possibility of separation. Therefore, any LM-OSL signal correlated with the 2 of Table 2 will be degenerated in one only component. In the present case this is the LM-OSL component C5, which obviously is complex and originates from the second component of the R-TL decay curves of peaks at 292°C, 353°C and 464°C.
. CONCLUSIONS
A component resolved bleaching analysis was conducted to the luminescence signal of commercial magnesium oxide. Bleaching took place at two different temperatures, namely at RT without any preheat as well as at 170°C after a preheat at 180°C, towards a quantitative relationship between the integrated signals of the TL-glow-curves and either the CW-OSL or LM-OSL curves. According to the data of the present study:
1) The integrated CW-OSL signal is much higher than the corresponding lost TL signal for both stimulation temperatures for stimulation times less than 20 s. However, as the stimulation time is increased, OSL and TL lost signal are of similar magnitude.
2) The analytical solution of the OTOR system of differential equations using the Lambert function W(z) provides de-convolution results with great accuracy for all cases of TL, CW-OSL and LM-OSL curves.
3) The fast OSL components C1 and C2 were monitored as consisting of electrons originated from all TL peaks. Therefore, these two components could not be correlated to any individual TL glow peak.
4) Component C3 is very well correlated with the TL peaks at 102, 135 and 194°C, while components C4 and C5 are directly correlated to the TL glow peaks of 292°C, 353°C and 464°C.
5) The dosimetric properties of components C4 and C5 should be further exploited.