. Introduction
Optically stimulated luminescence (OSL) dating of sediments associated with glacial advances in formerly glaciated areas is of importance for many palaeoenvironmental studies. One obvious scope is to reconstruct the timing and extent of glacial advances and by this contribute to the reconstruction of the regional palaeoclimate. Another valuable scope is to relate the sediment age to pedogenesis, as glacial advances provide fresh parent material for soil formation. The former Rhone-Aare-glacier in northern Switzerland is considered a key location for investigating pedogenesis in relation to sediment age, but a robust chronology for the sediments is still needed. A major potential problem in the dating of sediments from glacial environments results from potential incomplete bleaching of the OSL signal prior to deposition (Spencer and Owen, 2004; Duller, 2006; Preusser et al., 2007), which will lead to overestimation of the burial age if not detected and corrected for. As quartz is more readily bleachable than feldspar (Godfrey-Smith et al., 1988; Murray et al., 2012), it is the preferred mineral for such sediments. Furthermore, OSL measurements at a single grain scale have proven to be a powerful tool in assessing if a deposit suffers from partial bleaching (e.g. Olley et al., 2004; Duller, 2006). Here, the methodology is far more advanced and better understood for quartz in comparison to feldspar. However, several studies dealing with OSL dating of alpine quartz have reported problems with low signal intensities (Klasen et al., 2007, 2016; Preusser et al., 2007; Bickel et al., 2015; Lowick et al., 2015; Rades et al., in press). This phenomenon appears to be common for sediments originating from geologically young orogenies and might be explained by the lack of natural signal sensitisation through multiple cycles of bleaching and dosing prior to deposition (Moska and Murray, 2006; Preusser et al., 2006; Pietsch et al., 2008). While some studies point out additional problems with dating northern alpine quartz due to unstable signal components (Klasen, 2008; Klasen et al., 2016; Bickel et al., 2015), other studies do not observe such problems (Gaar et al., 2014; Salcher et al., 2015; Schielein et al., 2015). This might be explained by the complex geological composition of the Alps and related differences in the origin (magmatic versus metamorphic) and history of quartz grains in different regions. For example, quartz derived from sedimentary rocks may have undergone several depositional cycles in the past. Hence, it is crucial to test each catchment individually and this study aims to carefully assess the suitability of quartz from the area of the former Rhone-Aare-glacier.
In order to appropriately address potential problems with signal composition, small aliquot measurements were carried out, as their signals can be properly analysed in respect to the component composition. This analysis of the component composition is considerably more complicated for single grain signals, as the signal decay might rather reflect the degree of laser-grain coupling than true decay rate (Thomsen et al., 2012; 2015). Together with standard tests (preheat dose recovery tests, dose recovery test) of the Single Aliquot Regenerative Dose (SAR protocol), signal component analysis was conducted using mathematical deconvolution (McKeever and Chen, 1997; Bulur, 2000), and fast ratios were determined (Durcan and Duller, 2011). The effect of the signal composition was investigated by using the fast ratio as a rejection criterion in different ways and by choosing different background integral intervals (early background approach, Ballarini et al., 2007; Cunningham and Wallinga, 2010). Even though the small aliquot signals were dim and are likely to originate from only a small fraction (<10%) of all quartz grains (e.g. Duller et al. 2000), additionally, single grain analyses were carried out in order to check if the samples are affected by partial bleaching, that could not be detected in the small aliquot datasets.
. Materials and methods
The study was performed on nine samples chosen from a set of ~40 samples that were collected from the research area. Seven samples originate from deposits that are associated with the last glacial advance of the Rhone-Aare-glacier on the Swiss Plateau (outwash deposits), and two samples are taken from deposits formed by periglacial processes such as slope wash and solifluidal transport (Table S1, supplementary material). The sediments originate from bedrock in the source areas of the Rhone-Aare glacier, which comprise a large variety of rock types, including plutonic (granitic) basement and metamorphic rocks of the core of the Alps, carbonates and clastic sediments of the Prealps (Helveticum), and sandstones of the Molasse Basin. As the latter represent debris eroded during the main orogenesis, the origin of grains will also be complex.
Samples were collected by inserting stainless steel tubes into the vertically exposed sediments. They were prepared under subdued red light to avoid depletion of the natural OSL signal. For equivalent dose (De) determination, samples were dry sieved to separate the 150–200 μm grain size fraction, followed by HCl and H2O2 treatment to remove carbonates and organics, respectively. A quartz and potassium-rich feldspar fraction was extracted using heavy liquids (2.70 g cm−3, 2.58 g cm−3), and the quartz was subsequently etched in 40% HF for 1 h. The etched quartz was treated with 30% HCl for 1 h to eliminate any acid-soluble fluoride precipitates, and sieved again to remove disaggregated quartz grains and partially etched feldspars. For small aliquot measurements, grains were dispensed onto stainless steel discs in diameters of 2 mm (~150 ± 50 grains). For single grain measurements, the grains were mounted on aluminium discs that hold 100 grains each in 300 mm diameter holes (B⊘tter-Jensen et al., 2003).
Luminescence measurements were carried out on a Ris⊘ DA-20 TL/OSL single grain reader fitted with an internal 90Sr/90Y beta-source. To account for possible spatial non-uniformity of the dose rate each position on the single grain disc was individually calibrated (Thomsen et al., 2005; Ballarini et al., 2006). Small aliquots were stimulated with blue (470 ± 30 nm) light emitting diodes (LEDs), single-grain OSL signals were stimulated using a green (532 nm) laser. Ultraviolet (UV) emissions were detected through a 7-mm-thick and 2.5-mm-thick Hoya U-340 filter for small aliquot and single grain measurements, respectively.
Equivalent dose (De) estimates were obtained using the SAR protocol described in Murray and Wintle (2000), complemented with an additional step to check for feldspar grains or inclusions (IR depletion ratio, Duller, 2003), and modified for the single grains by using stimulation with an IR laser. In order to evaluate the ability of the SAR-protocol to recover a known laboratory dose, a number of dose recovery tests were conducted on sample material previously exposed to a Sunlux Ambience UV lamp for 24 h. To identify any dependence of the recovered dose on temperature (Wintle and Murray, 2006), preheat dose recovery tests were conducted for large aliquots (6 mm) of sample STH01 and ABH09. The tests were performed at temperatures between 210 and 290°C, using four aliquots per temperature step (given dose ~80 Gy, test dose ~20 Gy). In order to further test the protocol and determine the spread of the recovered doses, dose recovery tests were carried out on 48 aliquots of sample ABH08 and RUM04 (given dose ~50 Gy and ~60 Gy respectively, test dose ~20 Gy). De values for small aliquots were determined using a single saturating exponential fit for the dose response curve and an instrument error of 1.5%. The measured signal was integrated over the first 0.4 s. Aliquots were accepted if they had a natural signal more than 3 sigma above background, a test dose error < 15%, a recuperation signal (as % of highest given dose) < 5%, a recycling ratio that did not deviate more than 10% from unity within errors and an IR depletion ratio > 0.8.
For single grains, dose recovery tests were performed on four samples (ABH07, ABH07, AM01, and DM02). De was determined using a single saturating exponential fit for the dose response curve, an instrument error of 2.5% and the signal was integrated over the first 0.05 s. Grains were accepted if they had a test dose error < 15%, a recuperation signal (as % of highest given dose) < 5%, a recycling ratio not deviating more than 10% from unity within errors and an IR depletion ratio > 0.6. We chose this lower IR depletion ratio threshold for the single grain measurements than for the small aliquot measurements as, for most samples, there is a clear gap in IR depletion ratios between ~0.4 and 0.6 – making it straightforward to distinguish between pure quartz and feldspar grains/grains with feldspar inclusions (Fig. S1, supplementary material).
It has been shown that the quartz OSL signal consists of a number of discrete components (Smith and Rhodes, 1994; Bailey et al., 1997; Jain et al., 2003), which are characterized by unique thermal and optical properties. In order to quickly assess the component composition of the signals, we determined the fast ratio (Durcan and Duller, 2011). The fast ratio compares the intensity of the initial signal on an OSL decay curve, which should be dominated by the fast component, with an integral further along the decay curve chosen to represent the contribution of the medium component (Durcan and Duller, 2011). The fast ratio was calculated for the natural and the regenerated signal (measured after giving the second laboratory dose of the SAR protocol) of each aliquot. Durcan and Duller (2011) recommend the use of signal from the first channel to represent the fast ratio, because the relative contribution from the fast component to the total signal at this point will be at a maximum. We chose to increase this integral to 0.4 s, which is also the integral used for De determination in this study, as our signals are very dim and this reduces the associated error due to counting statistics. Although this lowers the fast ratio values, the precision is improved and the relative differences between the signals become more meaningful.
. Results and discussion
Performance tests and De determination
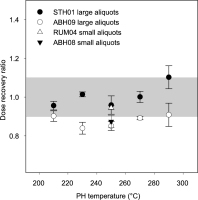
Fig. 1 shows the results of the preheat dose recovery test using large aliquots. There appears to be no relationship between preheat temperature and recovered dose, but recovery ratios are generally low for sample ABH09 (around 0.9). This is why, for the following dose recovery tests on small aliquots and single grains, a preheat of 250°C for 10 s was chosen. The results of the small aliquot dose recovery tests reveal, similar to the preheat dose recovery test, that the recovered dose of one sample (ABH08) slightly underestimates the given dose. The recovered dose distribution of this sample is characterized by an overdispersion (OD) of 18%, whereas for the second sample (RUM04) the given dose is recovered within errors and no OD is observed. This differences in OD may be due to different intrinsic characteristics of the samples. For single grains, recovered doses are 0.90 ± 0.03 (ABH07), 0.89 ± 0.05 (ABH08), 1.10 ± 0.04 (AM01) and 0.91 ± 0.05 (DM02) with OD values ranging between 11 and 23%.
Figure 1
Results of the preheat dose recovery tests (large aliquots) for sample STH01 and ABH09 and the small aliquot dose recovery tests for sample RUM04 and ABH08. Large aliquot dose recovery ratios were calculated using the arithmetic mean with standard error, small aliquot dose recovery ratios were calculated using the Central Age Model (CAM).
Of the measured small aliquots for De determination, about half of them do not pass the acceptance criteria (see Table 1). Between 0 and 31% of the measured aliquots do not exhibit a natural signal more than 3 sigma above background and/or a test dose error < 15%, additionally, between 17 and 54% do not pass the recycling ratio and/or IR depletion ratio acceptance criterion. Small aliquot signals usually do not approach saturation (they do not exceed 2D0).
Table 1
Small aliquot data. N = number of aliquots measured, n = number of aliquots used for De calculation, OD = overdispersion, De - CAM = equivalent dose calculated using the Central age model by Galbraith et al. (1999), A = to select aliquots for De calculation conventional rejection criteria were applied as described in chapter 2, B = individuals Des were determined using an early background and conventional rejection criteria were applied, C = conventional rejection criteria were applied and additionally all aliquots with FRnat ≠ FRreg were excluded, D = conventional rejection criteria were applied and additionally all aliquots with FRnat and FRreg < 15 were excluded.
Of the measured single grains, only a very small percentage (between 0.6 and 3.2%, depending on the sample) is accepted for De determination. Between 94.0 and 98.9% of the grains are rejected because they do not exhibit a natural signal more than 3 sigma above background and/or a test dose error < 15%. A smaller percentage (between 0.3 and 3.6%) are additionally rejected, because they do not meet the recuperation, recycling and/or IR depletion ratio criterion. At last, between 0 and 0.3% of the grains are additionally rejected because their De values were above 2D0 or oversaturated. For all samples the De values were routinely plotted against signal intensity but no relationship is observed.
Signal composition of small aliquot signals
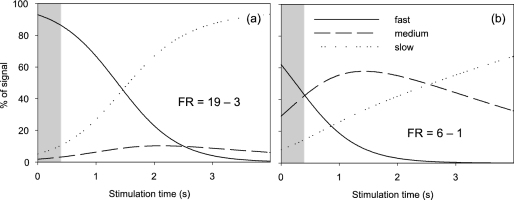
Fig. 2 shows the component composition for an aliquot signal with a high and a low fast ratio assessed by mathematical deconvolution (McKeever and Chen, 1997; Bulur, 2000). The higher the fast ratio, the more the initial signal is dominated by the fast component. According to Durcan and Duller (2011), in signals with a fast ratio > 10 the fast component contributes > 80%, while in signals with a fast ratio > 20, the contribution of the fast component is > 90%.
Figure 2
Mathematically deconvoluted signals of (a) a signal with a high fast ratio (FR = 19 ± 3) and (b) a low fast ratio (FR = 6 ± 1). Shaded area represents the time integral over which the initial signal was integrated (0.4 s).
A large number of the calculated fast ratios are relatively low (< 10), i.e. the fast component in the initial signal is less than ~80% (Durcan and Duller, 2011). For up to half of the aliquots per sample, there is a discrepancy between the fast ratios of natural and regenerated dose signals, the fast ratios do not agree within errors. Fig. 3 shows the determined fast ratio for the natural signal plotted against the fast ratio of the regenerated signal for each aliquot of sample ATH01 and STH01. Such an observed discrepancy between the component contributions may indicate the presence of a component that is thermally unstable (Li and Li, 2006; Steffen et al., 2009), has a high recuperation (Jain et al., 2003), sensitised differently during the SAR protocol (Jain et al., 2003), or is bleached to a different degree than the other components before burial (e.g. Bailey, 2003). These phenomena may also be a problem for aliquots where fast ratios agree within errors, but may not be visible due to their competing effects.
Figure 3
Fig. 3. Fast ratio for the natural signal plotted against the fast ratio of the regenerated signal for each aliquot of sample ATH01 (a) and STH01 (b). White dots show aliquots with an IR depletion ratio > 0.8, black dots show aliquots with an IR depletion ratio < 0.8.
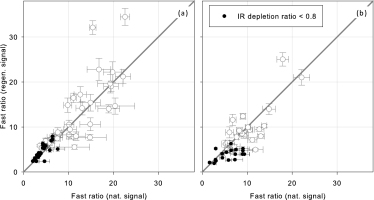
All aliquots with an IR depletion ratio <0.8 also exhibit a fast ratio <10 (Fig. 3, black dots). Feldspar contamination for these samples can therefore be excluded by either using the IR depletion ratio or the fast ratio as a rejection criterion, as has also been suggested by Fu et al. (2015). However, when using the latter criterion, aliquots with non-contaminated signals are also automatically rejected, which may be unnecessary.
Effects of signal composition on small aliquot De
The small aliquot De distributions following the conventional rejection criteria (Chapter 2) are normally distributed to slightly positively skewed (skew < 0.7) and display OD values between 27 and 39% (Table 1). As the signal component analysis has shown that many of the signals exhibit a rather weak fast component, its effect on the De determination was investigated. A dominant fast component in the OSL signal is one of the underlying assumptions when using the SAR protocol for quartz OSL dating (Wintle and Murray, 2006).
One way to explore the effect of the signal composition on De determination is to apply the early background (EBG) approach (Ballarini et al., 2007, Cunningham and Wallinga, 2010), where the signal measured immediately following the initial portion of signal decay is used to calculate the background. This is done to minimise the influence from any medium and slow components, and leaves a net signal dominated by the fast component. We used an EBG interval immediately following the initial signal interval and 2.5 times its duration as suggested by Cunningham and Wallinga (2010). For the small aliquot signals, this represents the first 0.4 s and a background averaged over the 0.5–1.4 s interval of signal decay. Applying this approach to the small aliquot dose recovery tests slightly increases the dose recovery ratio of sample ABH08 from 0.88 ± 0.03 to 0.90 ± 0.04, although the ratios still agree within errors. For sample RUM04 the ratio slightly decreases from 0.95 ± 0.01 to 0.93 ± 0.02 and the OD increases from 0 to 7%.
Another approach to explore the effect of component composition is to introduce the fast ratio as an additional acceptance criterion and two approaches are potentially useful in this context. One possibility is to reject all aliquots with a significant discrepancy between fast ratio of the natural and the regenerated signal (values do not agree within errors). This strategy assumes that a weak fast component in the initial signal is not necessarily a problem as long as the component composition is similar in the fast and the regenerated signal (as this is a sign of their stability and similar sensitisation during the SAR protocol). Any competing effects that might average out the influences on the components are not considered in this approach. Applying this criterion to the small aliquot dose recovery test increases the dose recovery ratio of sample ABH08 from 0.88 ± 0.03 to 0.92 ± 0.03 and leaves the dose recovery ratio of sample RUM04 unchanged.
Another possibility is to set an acceptance threshold for the fast ratio that both the natural and the regenerated signal should meet. Durcan and Duller (2011) recommend the use of a fast ratio threshold of 20 to guarantee reliable dating. Other studies have used lower thresholds (e.g., Fu et al., 2015; Feathers, 2015) following the suggestion of Duller (2012) to analyse the average De as a function of fast ratio and then choose a fast ratio threshold at which the De outcome is stable. Feathers (2015) observes a stable De beyond a threshold of 2 for his single grain data, and Fu et al. (2015) observe a stable De beyond a threshold of 15 for small aliquot data but without applying the IR depletion ratio as a rejection criterion. In this study we applied different fast ratio thresholds to our dose recovery data in order to identify a fast ratio threshold that is appropriate for testing the De determination. The dose recovery ratio of sample RUM04 appears to be independent of the fast ratio threshold and OD (as the latter was already 0% without applying any fast ratio threshold). It should be noted, however, that applying a threshold of 15 leaves only four values. The dose recovery ratio of sample ABH08 increases slightly from 0.88 ± 0.03 to 0.92 ± 0.04 beyond a fast ratio threshold of 14. We cannot exclude that this is simply coincidental, but despite this, a fast ratio of 15 is considered appropriate for testing the effect of signal composition on De determination as increasing the threshold above this, reduces the number of accepted aliquots to a number that prevents a robust calculation of the De. A fast ratio of 15 corresponds to a fast component contribution to the initial signal of > 85% (Durcan and Duller, 2011).
Fig. 4 compares the results of De determination using the different approaches described above (A – conventional approach, B – EBG approach, C – fast ratio of natural and regenerated signal agree within errors, D – fast ratio of natural and regenerated signal > 15). For most samples the calculated Des using the different approaches agree within errors, suggesting that signal composition has no significant effect on De determination. For those samples where the outcome differs slightly (RUM04, ATH04, DM02) there is no clear pattern (systematic increase or decrease of De) and may be due to a dramatically reduced dataset.
Figure 4
Small aliquot (A–D) and single grain (E–F) De values obtained with different approaches and for samples in this study. n = number of aliquots used for De calculation; filled symbols = De calculated using the Central age model (Galbraith et al., 1999); open symbols = De calculated using the Minimum Age Model (MAM3, sigma b = 0.3) (Galbraith et al., 1999); A – conventional rejection criteria; B – EBG approach, C – rejection of aliquots with fast ratio (natural) ≠ A fast ratio (regen); D – rejection of aliquots with fast ratio (natural) and/or fast ratio (regen) < 15; E – conventional rejection criteria; F – EBG approach. Horizontal lines extending the results of approach A are added for easier comparison of values.

Signal stability of small aliquot signals
The results of the previous section suggest that the signal composition does not influence the outcome of De determination, and imply that even signals with a strong medium component are suitable for dating. It was already concluded by Bailey (2010) that the absence of a strong fast component is not necessarily problematic as the thermal stability of the signal is essential in this context. Isothermal decay measurements (Murray and Wintle, 1999) using continuous wave OSL (CW-OSL) were conducted to identify the lifetime of the signal at varying temperatures for sample ABH09 and STH01. A set of 8 small aliquots (2 mm) per sample was first used for De determination and then given a dose of ~100 Gy, followed by a preheat of 250°C for 10 s (as for De determination). Similar to the approach of Buechi et al. (2017), the aliquot was then held for various times, between 0 and 5000 s, at elevated temperatures of between 220 and 280°C, after which the remaining signal was measured, followed by a 20 Gy test dose. For an ambient temperature of 20°C, lifetimes range between 1.1 ± 0.1 and 51 ± 1 Ma; (Fig. 5). It is not clear if this variability is due to intra-sample variability or to the measurement procedure. A lifetime of at least 20 times that of the burial age of a sample is recommended to avoid age underestimation due to loss of signal over time (Aitken, 1998), and this would suggest that already samples of > 50 ka may be affected by age underestimation. However, the present mean annual temperature on the Swiss Plateau is around 9°C and was certainly lower during most of the last 100 ka. Therefore, lifetimes at 10°C are considered more appropriate in order to evaluate if signal instability poses a problem for the samples investigated here, and would lead to a range of lifetimes between 8.2 ± 0.7 and 510 ± 10 Ma. The lowest measured lifetime at 10°C (8.2 ± 0.7 Ma) suggests that the signal should be stable for at least 400 ka, indicating that the samples of interest (expected to be younger than 100 ka) are well within the reliable dating range.
Figure 5
Lifetimes calculated from isothermal decay measurements for sample ABH09 and STH01 at 10 and 20°C. Dotted line indicates the lifetime required for a stable signal of samples <100 ka (expected age of samples in this study).
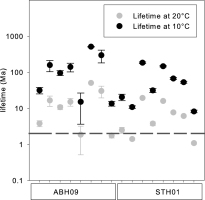
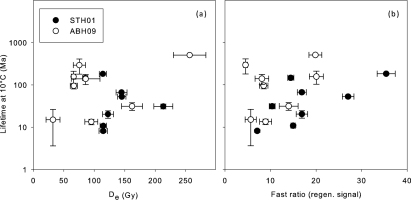
Fig. 6 shows the lifetimes at 10°C plotted against the previously determined De values and fast ratios of the regenerated signal. There is no apparent relationship between lifetime and De value, in agreement with the previously reasoned assumed stability of the quartz signal. There is a very vague positive correlation between lifetime and fast ratio (R2 = 0.43 and 0.18 for a linear regression), which may point to the influence of a thermally less stable or unstable medium component; where the medium component contributes significantly to the signal (low fast ratio), the overall signal stability is also lower.
Dose distributions
Six out of nine of the small aliquot dose distributions show a slight positive skew (skew 0.1–0.7, see Table 1) but at the same time OD values are moderate and relatively uniform (27–39%). Hence, it is difficult to decide if the samples are suffering from partial bleaching and single grain distributions were analysed to further investigate this issue.
Single grain measurements reveal that between 1 and 6% of the measured grains exhibit a signal more than 3 sigma above background and a test dose error < 15%. Besides, there is also a large number of dim grains that contributes to the total signal sum (Fig. S2 in the supplementary material). As one small aliquot contains 150 ± 50 grains at least part of the resulting signals will be affected by signal averaging. The single grain De distributions show rather large differences in shape and overdispersion, and for five of the nine samples the distributions are clearly skewed towards higher values, displaying overdispersion values of up to 74% (Table 2). The most likely explanation for the observed skewness combined with high overdispersion values is that samples were differentially bleached prior to deposition (Wallinga, 2002). This interpretation is supported by the fact that the samples are taken from sedimentary setting that are likely to be affected by partial bleaching (Fuchs and Owen, 2008).
Table 2
Single grain data. N = number of grains measured, n = number of grains used for De calculation, OD = overdispersion, Skew of De distribution following Bailey and Arnold (2006), De - CAM = equivalent dose calculated using the Central age model by Galbraith et al. (1999), E = to select aliquots for De calculation conventional rejection criteria were applied as described in chapter 2, F = individuals Des were determined using an early background and conventional rejection criteria were applied.
The Minimum Age Model (MAM, Galbraith et al., 1999) is considered appropriate for the calculation of mean De values for these samples. We also applied the MAM to sample STH01 although it is only slightly skewed, but with an OD of 69%. The sigma b value was chosen based on the average OD of the symmetric, and therefore likely to be “well-bleached” single grain distributions of the samples in this study. This is supported by Gaar and Preusser (2012) and Gaar et al. (2014), who suggest OD values of around 0.30 as input value for the MAM when analysing single grain quartz De distributions of samples from northern Switzerland.
Effects of signal composition on single grain De
Single grain measurements revealed skewed De distributions for five out of the nine samples which we interpret as an indication of partial bleaching. Nonetheless, it is important to also exclude the possibility that these distributions are the result of different signal composition characteristics (e.g. stable and unstable signals) instead. For the single grain signals, we considered the fast ratio and the EBG approach as possibilities to investigate the effect of signal composition on single grain De. The EBG approach was applied using the initial signal interval of the first 0.05 s and a background averaged over the 0.06–0.18 s interval of the signal. The fast ratio has been used in several single grain studies (e.g., Duller, 2012; Jacobs et al., 2013; Feathers, 2015), although its significance is considered problematic due to the uncertain power delivery of the green laser (Thomsen et al., 2012, 2015). In order to determine the fast ratio of the natural single grain signals of our samples, we chose the first 0.02 s to represent the fast component and the average signal over the 0.18–0.22 s interval to represent the medium component, following Feathers (2015) and Jacobs et al. (2013) who both use these intervals for 90% laser power. Given the afore mentioned difficulties, these integrals can only be considered approximate (Feathers, 2015). Due to the relatively dim signals, we encountered problems with large uncertainties, as well as negative and inflated values (cf. Durcan, 2012).
Fig. 7 shows the dependence of the single grain dose recovery ratios on fast ratio threshold and EBG approach, respectively. There is no obvious systematic dependence on fast ratio threshold nor on EBG approach. In Fig. 8 the single grain De distribution of sample ABH07 is displayed with filled symbols showing grains with natural signals that exhibit a fast ratio >20. There seems to be no significant change to the distribution by only using grains with fast ratios >20. As the calculation of the fast ratio for single grain signals leads to large uncertainties, and no clear effect in applying a fast ratio threshold is observed for the dose recovery ratios nor the De distributions, we decided to use only the conventional and EBG approach to calculate CAM and MAM doses for our single grain data (Fig. 5, Table 2). While the CAM doses using the conventional and EBG approach agree well, there is a tendency towards slightly younger MAM ages when applying the EBG approach. We assume that this may be explained by the reduced dataset. Despite this, the resulting MAM doses of both approaches agree within errors, and there is therefore no obvious reason to support the EBG approach over the conventional one for the samples of this study.
. Conclusions
A considerable number of the small aliquot quartz signals from the nine samples investigated in this study exhibit a weak fast component. Fast ratio analyses reveal that for a notable number of aliquots the signal composition between natural and regenerated signals differs significantly. Investigating the effects of signal composition on De shows that the latter is not dependent on whether these aliquots are excluded or not. Isothermal decay measurements confirmed that the small aliquot quartz signals are thermally stable over at least 400 ka at 10°C. The analysis of single grain quartz data reveals that signal averaging can be present even in the very dim small aliquot signals and some samples suffer from partial bleaching. Fast ratio analyses of the single grain signals – which can only be considered approximate – support our interpretation that the skewed single grain distributions are actually the result of partial bleaching and not of differences in signal composition of the single grain signals. We therefore recommend to investigate these samples on a single grain level to detect potential partial bleaching. Ideally, evidence of partial bleaching shown by skewed De distributions should be backed up by comparison to feldspar dating.