. Introduction
Recently, optically stimulated luminescence (OSL) has been proposed as a geochronological tool applicable to rock surfaces (e.g. Vafiadou et al., 2004; Simms et al., 2011; Liritzis, 2011; Sohbati et al., 2011, 2012, 2015; Chapot et al., 2012; Freiesleben et al., 2015). OSL dating techniques have been predominantly developed for quartz and feldspar as target minerals. Although the quartz luminescence signal is more stable than that of feldspar (Aitken, 1985), it is not always possible to find samples with a useful quartz sensitivity when dating solid rocks (Sohbati et al., 2011; Guralnik et al., 2015). In addition, it is difficult to separate pure mineral phases in igneous rock slices without losing grain-size dependent dosimetric information (Sohbati et al., 2011); however earlier studies have shown that the infrared stimulated luminescence (IRSL) signal in blue emission band from coarse grains is mainly associated with K-rich feldspar (e.g. Baril and Huntley, 2003; Sohbati et al., 2013). Unfortunately, the conventional IRSL signal suffers from anomalous or athermal fading (Wintle, 1973; Aitken, 1985; Spooner, 1994) and as a result has proved to be of limited value in dating. However, the feldspar signal derived from infrared stimulation at elevated temperature, measured after stimulation at about 50°C or higher temperature (the so-called post-IR IRSL or pIRIR; Thomsen et al., 2008; Buylaert et al., 2012; Li and Li, 2012a) seems to circumvent this problem and offers considerable potential for the dating of older material. Over the last few years, the pIRIR signal from feldspar has been increasingly applied to the dating of different types of sedimentary samples (e.g. Buylaert et al., 2009; Li and Li, 2011; Thiel et al., 2011), but there is little information on the performance of the single-aliquot regeneration-dose (SAR) measurement protocol (Murray and Wintle, 2000) on the pIRIR signal from rock slices.
The size of the test dose (e.g. Qin and Zhou, 2012; Buylaert et al., 2012; Yi et al, 2016) and the stimulation temperature (e.g. Thomsen et al., 2008; Li and Li, 2012b) are important parameters in pIRIR dating. In this study, we investigate the effect of test-dose size and first stimulation temperature on the pIRIR290 signals from rock slices, especially from those close to saturation. This is undertaken using both natural and laboratory saturated samples.
. Sample and Measurement Instrument
Aliquots were taken from a glacial granite gneissic boulder (MUST88) sampled in July 2013 from the Pamir plateau, Western China (Fig. 1) previously dated to ~80 ka by Seong et al. (2009) using 10Be. Several blocks of ~4×4×7 cm were cut from the surface of the boulder using a petrol-driven cut-off saw equipped with a diamond blade. Sample preparation and luminescence signal measurements were carried out at the Institute of Geology (China Earthquake Administration, China) and at the Nordic Laboratory for Luminescence Dating, Aarhus University, Denmark and Center for Nuclear Technologies (DTU Nutech), Technical University of Denmark. Under subdued red-orange light, cores ~10 mm in diameter and up to 40 mm long were drilled from these blocks using a water-cooled diamond core drill; these cores were then cut into 1.2 mm thick slices using a water-cooled low-speed saw equipped with a 0.3 mm thick diamond wafer blade, giving a net slice spacing of 1.5 mm. The surface slices were treated with 10% HF for 30–40 min and 10% HCl for 20 min to remove any weathering products. No treatment was undertaken on inner slices (Sohbati et al., 2011).
Fig. 1
(a) Study area located at the western part of China, Pamir Plateau. (b) Samples were taken from the SW side of the Muztagh Ata massif. This fig was modified after the Fig. 1A in Owen et al., (2012). (c) Photo of the glacial gneissic boulder (MUST 88) from which the sample was taken (Seong et al., 2009).
Rock slices were put in a carousel directly and measured on a Risø TL/OSL reader Model DA-20, using infrared stimulation (870 nm, ~130 mW/cm2) and photon detection through a Schott BG 39/Corning 7-59 filter combination (2 and 4 mm, respectively). Beta irradiation used a calibrated 90Sr/90Y source mounted on the reader (Bøtter-Jensen et al., 2010).
. Methods and Results
Luminescence characteristics of IR50 and pIRIR290
The measurement protocol shown in Table 1A (modified after Thiel et al., 2011) was used to measure the IR50 and pIRIR290 signals. For calculations employing a net signal, the initial 2 s of the signal minus a background evaluated from the last 10 s of the 200 s stimulation was used. Fig. 2a shows the natural IR50 and pIRIR290 decay curves for one slice from a depth of ~30 mm into the rock surface from a single core. Fig. 2b shows the sensitivity-corrected natural IR50 and pIRIR290 signal (Ln/Tn) of slices plotted against depth, normalized to the average Ln/Tn at depths >15 mm. Negligible signal was detected up to a depth of ~8 mm for IR50 and ~4 mm for pIRIR290 into the rock, because of zeroing of the signal near the surface. Based on the fitting of the simple rock-surface-exposure model (Equation 5.5 from Sohbati et al. 2011; the solid curves), the IR50 and pIRIR290 signals are in field saturation at depths >12 mm and >10 mm, respectively. The values at these depths are scattered, presumably because of variability in the Do across the slices. However, the individual pIRIR290 Ln/Tn values from these depths lie very close to the saturation level in their respective laboratory dose response curve (Fig. 2a inset), while the natural IR50 signal (solid symbols) is ~50% of laboratory saturation.
Fig. 2
(a) Typical decay curves and (inset) dose response curves of IR50 (dashed line) and pIRIR290 (solid line) signals. (b) The variation of the IR50 and pIRIR290 “residual signals” with depth into the rock surface.
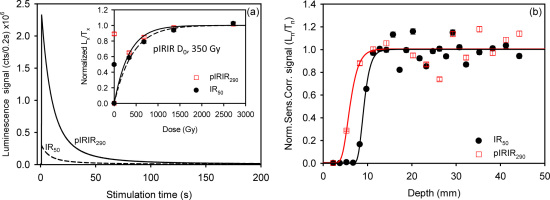
Table 1
The post-IR IRSL SAR protocols used in this study
| Step | A | B | C3 |
|---|---|---|---|
| 1-1 | Natural or Regeneration dose | Dose (4400 Gy) | Natural, Natural+2688 Gy, bleached+2688 Gy or Regeneration dose |
| 1-2 | Preheat at 320°C for 100 s | Preheat at T°C for 100 s 1 | Preheat at 320°C for 100 s |
| 1-3 | IR at 50°C for 200 s (Lx,50) | IR at 50°C for 200 s (Lsat, 50) | IR at T °C for 200 s 2 |
| 1-4 | IR at 290°C for 200 s (Lx,290) | IR at (T-30)°C for 200 s (Lsat, T-30) | IR at 290°C for 200 s (Ln or Lsat) |
| 1-5 | IR at 50°C for 200 s (Linherited, 50) | ||
| 1-6 | IR at (T-30)°C for 200 s (Linherited, T-30) | ||
| 2-1 | Test dose | Test dose | |
| 2-2 | Preheat at 320°C for 100 s | Preheat at 320°C for 100 s | |
| 2-3 | IR at 50°C for 200 s (Tx,50) | IR at T °C for 200 s | |
| 2-4 | IR at 290°C for 200 s (Tx,290) | IR at 290°C for 200 s (Tn or Tsat) | |
| 3-1 | IR at 325°C for 200 s (Thermo-optical wash) | IR at 325°C for 200 s (Thermo-optical wash) | |
Inheritance in the test dose response
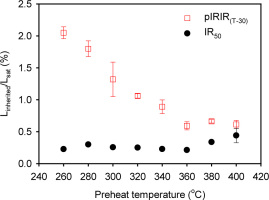
At high doses, even a small residual remaining after the measurement of Lx signals could significantly affect the signals from small test doses and so have an effect on the final De estimate (e.g. Qin and Zhou, 2012; Nian et al., 2012; Fu et al., 2015). We first investigated the size of any inherited signal arising due to thermal transfer and/or insufficient zeroing during measurement of the Lx signals, using the sequence outlined in Table 1B. After measurement of the natural signal from various slices and thermo-optically bleaching (IRSL for 200 s at 325°C) any remaining signal, a high regeneration (4400 Gy) dose was given to each slice, which were then measured according to Table 1B. Fig. 3 shows the ratio of the inherited IR50 and pIRIR signals (steps 1–5, 1–6, Table 1B) to the corresponding initial signals (steps 1–3, 1–4) plotted against preheat temperature. For the IR50 signal this ratio is consistently ~0.2% except at the highest two preheat temperatures (>360°C) where this ratio begins to increase to a maximum of ~0.5% at 400°C. In contrast, the inherited pIRIR signal decreases with temperature from ~2% at 260°C to ~0.6% at 360°C. Assuming that the dose response curve follows an exponential growth, an inherited signal of 2% corresponds to an inherited dose of ~7 Gy (using the Do of 350 Gy from Fig. 2 inset). This implies that for samples recording a large dose resulting in signals at or close to saturation, any test dose should be significantly larger than 7 Gy. This is discussed further below (next section).
Fig. 3
The ratio of the “residual signal” (steps 1-5, 1-6, Table 1B) to the initial signal (steps 1-3, 1-4) at different preheat and stimulation temperatures. Three slices were measured at each temperature. The error bars represent one standard error.
Measuring rock slices in saturation: effect of test dose size and the order of regeneration dose
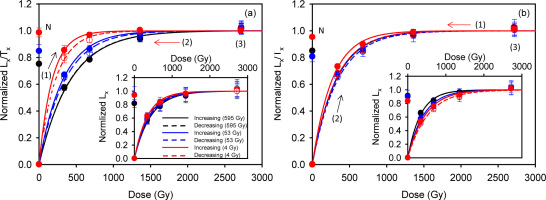
Six sets of experiments were undertaken to test the influence of test dose on the pIRIR290 dose response curves and the accuracy of the measured equivalent doses; these involve changing the order in which the regeneration doses were given (Tso and Li, 1994; Timar-Gabor and Wintle, 2013), and the size of the test dose. Three saturated slices from the inner part of rock core (depth >15 mm) were used for each set of experiment (i.e. 18 naturally saturated slices in total). The Lx/Tx results are shown in Fig. 4, normalized to the saturation value of their corresponding fitted dose response curve (single saturating exponential function). The insets show the Lx data alone without test dose normalization. In Fig. 4a, 4c, 4e, after the measurement of the natural signal, the regeneration doses were (1) given in increasing order, then (2) repeated, but in decreasing order, and finally in step (3) the highest dose (~2700 Gy) was repeated again. In the second group of experiments (Fig. 4b, 4d, 4f), the regeneration doses were (1) first given in decreasing order and then (2) in increasing order before (3) the highest dose was re-measured. In Fig. 4a and 4b, the test dose was on ly 4 Gy. These experiments were repeated with a larger test dose of 53 Gy to give Fig. 4c and 4d, and a much larger test dose of 595 Gy to give Fig. 4e and 4f.
Fig. 4
Laboratory dose response curves for different test doses, where the regeneration doses are given in increasing or decreasing order. For (a) and (b) the test dose is 4 Gy, (c) and (d) -53 Gy, and (e) and (f) ~595 Gy. The solid and dashed lines represent doses given in increasing and decreasing order, respectively. The numbers (1), (2) and (3) show the order in which the regeneration doses were given. Three slices were measured at each point. The insets show the dose responses of the sensitivity uncorrected signal (Lx). All data were normalized to the saturation value of their corresponding fitted dose-response curve. The Do values corresponding to the solid Lx/Tx curves, based on a single saturating exponential fit, are presented in the individual figures.
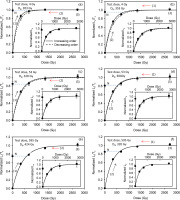
Comparison of the shapes of the dose response curves suggests that in the first group of experiments (regeneration doses first given in increasing order) the value of Do increases with the size of the test dose (Fig. 4a, 4c, 4e). However, there is no such correlation in the second group where the regeneration doses were initially given in a decreasing order; here Do seems to be independent of the test dose size (Fig. 4b, 4d, 4f). For clarity all the dose response curves are summarized in Figs. 5a and 5b. Although the potential natural variation in the Do values of individual slices as implied from the luminescence-depth profile (see Fig. 2b) may preclude any conclusive interpretation of these data, this observation is nevertheless noteworthy because each dose response curve is an average of three curves measured from three different naturally saturated slices.
A further comparison of the sensitivity-corrected dose response curves constructed by giving doses in increasing and decreasing order (in the same experiment) indicates that their reproducibility improves as the test dose increases (Fig. 4a-f; note the discrepancies between the solid and dashed curves). The reproducibility is poorer when a small test dose (4 Gy) is used to measure dose response curves up to saturation, and independent of the order in which regeneration doses are given (Fig. 4a and 4b). However, it becomes increasingly better when the test dose size is increased (Fig. 4c, 4d, 4e, 4f). In Fig. 4e, 4f, with the largest test dose (595 Gy), the solid and dashed curves overlap.
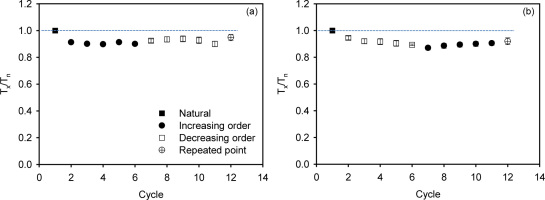
Although the natural signal appears to be closer to saturation in the dose response curves that have not been corrected for sensitivity change (Fig. 4 insets), this is likely to be an artefact of sensitivity change; Fig. 6 shows that the test-dose response drops by ~10% between the natural and the first regeneration SAR cycle. When the Lx/Tx data are examined (Fig. 4), the natural signal lies 1% (Fig. 4a) and 5% (Fig. 4b) below laboratory saturation for the 4 Gy test dose, 15 (Fig. 4c) and 19% (Fig. 4d) below for the 53 Gy test dose, and 25 (Fig. 4e) and 15% (Fig. 4f) below for the 595 Gy test dose. The apparent saturation (or close to saturation) of the natural signal for the 4 Gy test dose is possibly a reflection of the inheritance effect discussed above.
Effect of first IR stimulation temperature
In this experiment, three groups of slices were measured, where the first IR stimulation temperature was 50°C, 200°C or 250°C (Fig. 7, Table 1C). The purpose of this experiment is to see which prior treatment gives the most reliable dose estimate. Group (1) consisted of naturally saturated slices from the inner part of the rock (depth >15 mm). Group (2) contained naturally saturated slices from the inner part of the rock to which a high dose of 2688 Gy had been added. Group (3) contained naturally bleached slices from the surface of the rock to which a high dose of 2688 Gy was added. All these samples were then measured and “Ln/Tn” (first cycle measurements resulting from natural, natural+2688 Gy, or bleached+2688 Gy, as appropriate) were derived. Subsequently, a regenerated dose cycle with 2688 Gy was undertaken using all these slices; this cycle gave an estimate of the laboratory saturation signal Lsat and its corresponding test dose response Tsat. The ratios of the “Ln” to Lsat and “Ln/Tn” to Lsat/Tsat are shown as a function of first stimulation temperatures in Fig. 7, for two sizes of test dose, 53 Gy (Fig. 7a,7c) and 595 Gy (Fig. 7b,7d). These data are similar to those from a dose recovery test except that we are considering the reproducibility of light levels (luminescence intensities) rather than doses.
Fig. 7
Effect of first stimulation temperature on the degree of saturation. Test doses in (a) and (c) are ~53 Gy and in (b) and (d) ~595 Gy. The shadowed area covers 10% deviation from unity (i.e. 0.9 to 1.1). Three slices were measured at each temperature. The error bars represent one standard error.
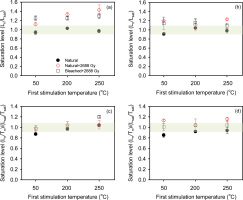
Consider first Fig. 7a, 7b where the uncorrected absolute light level ratios (Ln/Lsat) are presented. In both figures, the natural signals (Ln) are within 10% of the regenerated Lsat signals, suggesting that the natural light level is indistinguishable from the regenerated saturated light level, as was also indicated in Fig. 4 insets. However the ratios of Ln+2688/Lsat and Lbleached+2688/Lsat are all >1 (unfilled diamond and unfilled square symbols in Fig. 7a, 7b); this confirms that the apparent saturation of the natural signal is an artefact of the change in sensitivity during the measurement of the first SAR cycle (see Fig. 6 and discussion above). Fig. 7c, 7d present the sensitivity corrected ratios (Lx/Tx). Here most of the Ln+2688/Tn+2688 and Lbleached+2688/Tbleached+2688 signals are consistent with the corrected regenerated signals (Lsat/Tsat) at 2σ, indicating a good recovery ratio for samples saturated in the laboratory. However, for the naturally saturated slices (group 1), the signal is <0.9 for first stimulation temperature at 50°C. This effect is independent of test-dose size and could possibly be because we are sampling a less stable signal with a lower prior IR stimulation temperature. However, there is also a tendency for an increase in the levels of laboratory dosed Ln+2688/Tn+2688 and Lbleached+2688/Tbleached+2688 with a prior IR stimulation temperature, and in fact some data lie above unity; thus, the increase cannot be solely attributed to signal stability. Our data suggest that an apparent increase in the ratio with IR stimulation temperature could be a combination of both sensitivity change and increased stability. It may also be that the results obtained using a first stimulation temperature of 200°C are closer to unity that those obtained using 250°C, although at this stage we do not wish to place too much confidence in this conclusion.
. Discussion and Conclusion
We find that the reproducibility of the sensitivity-corrected dose response curve is poorer when a small test dose (4 Gy) is used to measure dose response curves up to saturation; however the small test dose gives the best agreement between the natural signal (expected to be in saturation) and the dose response curve. This result may be attributed to the inheritance effect, which can translate into a dose as high as 7 Gy (section 3 – Inheritance in the test dose response) and thus be a source of significant contamination in the test dose pIRIR290 signal. We are unable to detect a significant effect of inheritance in the comparison of the large 595 Gy and 53 Gy test doses in the subsequent experiments (reproducibility of laboratory dose-response curves, Fig. 4, or first to second cycle saturation light level ratios, Fig. 7). This is presumably because even the 53 Gy test dose was >7 times larger than any potential inheritance. Fig. 4c–f indicates that laboratory measurements of dose-response curves are reproducible and, when the test doses are much larger than the inheritance dose (7 Gy) in any given experiment, the resulting dose-response curves are independent of the order in which regeneration doses are given. Perhaps surprisingly this is equally true of absolute light levels (Fig. 4 insets) and Lx/Tx ratios. Although it appears that the absolute light levels (Lx) give natural signals closer to saturation, we argue that this is an artefact of a significant change in sensitivity especially in the first SAR cycle (Fig. 6). This argument is supported by the comparison of the non-normalized and test-dose normalized ratios of the “natural” to laboratory saturation levels (Fig. 7). Although the non-normalized ratios are close to unity for the natural signal, these ratios are up to 1.4 (Fig. 7a) for the samples which were saturated in the laboratory (Ln+2688/Lsat and Lbleached+2688/Lsat) before the first measurement cycle (test dose), clearly indicating a significant change in sensitivity. This is in contrast to the ratios of the test-dose normalized data which are generally much closer to unity, although there remains some underestimate for a first stimulation temperature of 50°C. It is interesting to note that Li and Li (2012a) and Yi et al. (2016) have both observed an underestimation in De plateau for a first stimulation temperature of 50°C, although several authors (e.g. Buylaert et al., 2012, 2015; Yi et al., 2015) have shown that natural doses up to 650 Gy are independent of first stimulation temperature. It may be that the underestimates derived from the test-dose corrected natural saturation light levels (Fig. 7for a first stimulation temperature of 50°C) only become significant for large palaeodoses.
Our data indicate that there is a systematic increase in dose response curve saturation (or Do) with test dose size when the regeneration doses are first given in increasing order, and then decreasing order (Fig. 5a). This trend disappears if these orders are reversed (Fig. 5b). We do not at present understand this effect.
In conclusion, for our samples, it appears that when measuring large doses, (i) the saturation of the dose response curve changes as a function of the test dose if the regeneration doses are delivered in an increasing order, but this effect is not so important if the regeneration doses are delivered in the decreasing order, (ii) the size of the test dose should be significantly larger than the apparent dose corresponding to any carryover from the previous measurement, and (iii) it may be better to use a first stimulation temperature of at least 200°C for samples close to saturation, regardless of the size of the test dose.